Accueil
Lois
de Képler

Programme officiel (Extraits)

 

Démontrer que, dans l’approximation des trajectoires circulaires, le mouvement d’un satellite, d’une planète, est uniforme.

Établir l’expression de sa vitesse et de sa période.

Connaître les trois lois de Kepler ; exploiter la troisième dans le cas d’un mouvement circulaire.

 

 

Baccalauréat S physique-Chimie Métropole 2005 (extrait). Sans calculatrice.
   
 

Satellites terrestres artificiels.

Passionné d'astronomie, un élève a collecté sur le réseau Internet de nombreuses informations concernant les satellites artificiels terrestres. Il met en oeuvre ses connaissances de physique pour les vérifier et les approfondir.

Dans tout l'exercice, on notera :

Masse de la Terre : MT (répartition de masse à symétrie sphérique de centre O)
Rayon de la Terre : RT
Masse du satellite étudié : ms
Altitude du satellite étudié : h

Constante de gravitation universelle : G

 

1. Le premier satellite artificiel.

Si la possibilité théorique de mettre un satellite sur orbite autour de la Terre fut signalée en 1687 par Isaac Newton, il a fallu attendre le 4 octobre 1957 pour voir le lancement du premier satellite artificiel, Spoutnik 1, par les soviétiques.

1.1. Exprimer vectoriellement la force exercée par la Terre sur Spoutnik 1, supposé ponctuel, et la représenter sur un schéma.

1.2. L'étude se fait dans un référentiel géocentrique considéré comme galiléen.

En appliquant la deuxième loi de Newton établir l'expression vectorielle de l'accélération du satellite.

2. Les satellites artificiels à orbites circulaires.

Le télescope spatial Hubble, qui a permis de nombreuses découvertes en astronomie depuis son lancement en 1990, est en orbite circulaire à 600 km d'altitude et il effectue un tour complet de la Terre en 100 minutes.

2.1. Etude du mouvement du satellite Hubble dans un référentiel géocentrique.

En reprenant les résultats de la partie 1, montrer sans calcul que le mouvement circulaire de Hubble est uniforme.

 

 

 

Aide schématique à la résolution de l'exercice

 

     
Sujet et correction détaillée de l'extrait du sujet Métropole 2005

Accueil

     
Baccalauréat S physique-Chimie Antilles-Guyane 2014 (Extrait).
     
     

 

Estimation de la masse du trou noir.


Pour déterminer un ordre de grandeur de la masse M du trou noir, on considère dans cette question que l'étoile S2, de masse m, décrit une orbite circulaire de rayon r = 132 heures-lumière, la période de révolution étant T = 15,2 ans.

3.1 Schématiser la trajectoire de l'étoile S2 et représenter, en plusieurs points de la trajectoire, l'étoile, son vecteur vitesse, son vecteur accélération.
3.2 Montrer que la valeur v de la vitesse de l'étoile S2 a pour expression :
3.3 En déduire l'expression de la période de révolution T de l'étoile.
3.4 Déterminer la valeur de la masse M du trou noir et la comparer à celle annoncée dans le document 1.

Extrait du document 1 :

L'orbite d'une étoile particulière a permis de démontrer l'existence d'un trou noir (1) de 3 à 4 millions de masses solaires.
Masse du soleil : MS = 2,0 x 1030 kg

Le fait que la trajectoire soit restée purement képlérienne a ainsi permis d'éliminer définitivement toute possibilité que la masse de quelques millions de masses solaires soit sous forme d'un amas dense stellaire sombre.

 

 

Aide schématique à la résolution de l'exercice

 
     
Sujet et correction détaillée de l'extrait du sujet Antilles-Guyane 2014
     
Accueil
Baccalauréat S physique-Chimie Centres étrangers 2009 (Extrait).
     
     

Observation des satellites de Neptune par la sonde Voyager 2.

 

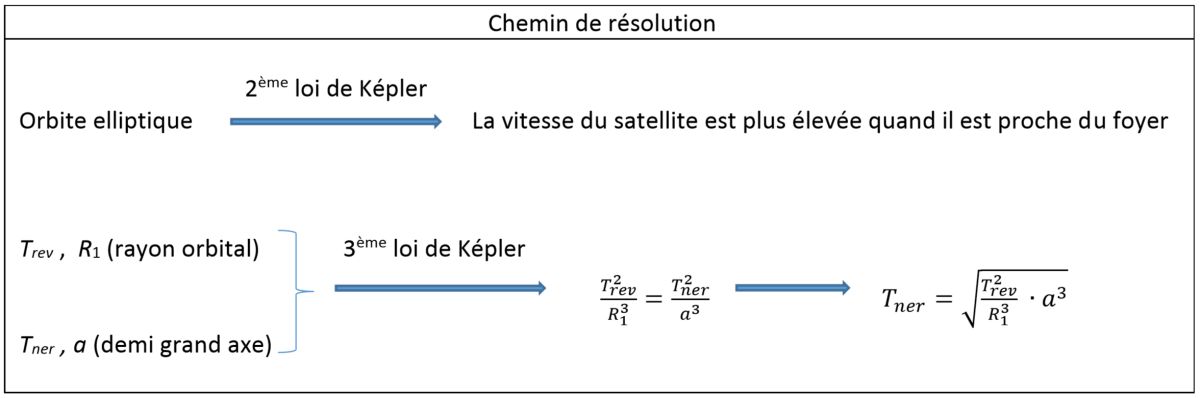
Extrait du texte introductif :

Neptune est le dernier et le plus lointain des mondes géants que la sonde Voyager 2 nous fit découvrir.
Neptune possède plusieurs satellites : Triton et Néréide figurent parmi les satellites les mieux connus.
C’est un satellite gros comme la Lune ; il mesure environ 4 200 km de diamètre.
L’orbite de Triton est circulaire autour du centre de Neptune.
Découvert en 1949, Néréide est au contraire assez petit (320 km de diamètre) et a une orbite très elliptique, la plus allongée de tous les satellites. Néréide met 360 jours pour boucler son orbite.

D’après un article publié sur le site du Club Astro Antares.

Extrait des données :

rayon orbital : R1 = 3,547 x 105 km
période de révolution :Trev = 5,877 jours solaires
Néréide : demi-longueur du grand-axe : a = 5513 x 103 km

Constante de gravitation : G = 6,67 x 10–11 m3.kg-1.s-2

1 jour solaire = 86 400 s.

1.4. On considère les aires balayées par le segment reliant Neptune à Néréide pendant une même durée en différents points de l’orbite.
Sur la figure ci-dessous, elles correspondent aux aires des surfaces formées par les points N, P1 et P2 autour du péricentre P d’une part et N, A1 et A2 autour de l’apocentre A d’autre part.

 

 

1.4.1. Quelle relation relie ces aires ?
1.4.2. Comparer alors les vitesses de Néréide aux points A et P.

 

1.5. On souhaite déterminer la période de révolution Tner de Néréide.

1.5.1. Énoncer la troisième loi de Képler.
1.5.2. Calculer la valeur de  en s2.m-3
1.5.3. À l’aide des questions précédentes, en déduire la période de révolution Tner de Néréide. Puis comparer à la valeur donnée dans le texte.

 

 

 

Aide schématique à la résolution de l'exercice

 
     
Sujet et correction détaillée de l'extrait du sujet Centres étrangers 2009
 
Accueil